Update Sudoku
This commit is contained in:
parent
ebc9f62f98
commit
e6dcb4f12c
456
ipynb/StarBattle.ipynb
Normal file
456
ipynb/StarBattle.ipynb
Normal file
@ -0,0 +1,456 @@
|
||||
{
|
||||
"cells": [
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"<div align=\"right\" style=\"text-align: right\"><i>Peter Norvig<br>Aug 2021</i></div>\n",
|
||||
"\n",
|
||||
"# Star Battle Puzzles\n",
|
||||
"\n",
|
||||
"If you thought this notebook was going to be about a video game like StarCraft®, I'm sorry to disapoint you. Instead it is about [**Star Battle puzzles**](https://www.puzzle-star-battle.com/), a genre of Sudoku-like puzzles with these properties:\n",
|
||||
"\n",
|
||||
"- Like Sudoku, you start with an *N*×*N* board and fill in cells.\n",
|
||||
"- Like Sudoku, an *N*×*N* board has 3*N* **units**: *N* columns, *N* rows, and *N* boxes.\n",
|
||||
"- Like Sudoku, a well-formed puzzle has exactly one solution.\n",
|
||||
"- Unlike Sudoku, the boxes have irregular shapes (not squares) and differing numbers of cells.\n",
|
||||
"- Unlike Sudoku, there are only 2 possible values for each cell: star or blank (not 9 digits).\n",
|
||||
"- Unlike Sudoku,\n",
|
||||
"- The constraints are:\n",
|
||||
" - Each unit (column, row, or box) must have exactly *S* stars.\n",
|
||||
" - Two stars cannot be adjacent (not even diagonally).\n",
|
||||
"\n",
|
||||
"\n",
|
||||
"\n",
|
||||
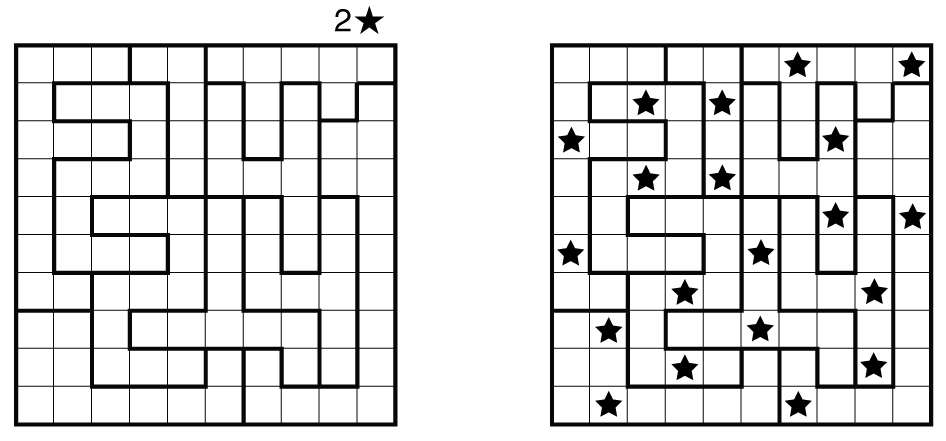
"Here is a board (*S*=2, *N*=10) and its solution from a helpful [Star Battle Rules and Info](https://www.gmpuzzles.com/blog/star-battle-rules-and-info/) page:\n",
|
||||
"\n",
|
||||
"\n",
|
||||
"\n",
|
||||
"This “24”-themed puzzle was created by Thomas Snyder for the 24-Hours Puzzle Championship in Hungary in 2012.\n",
|
||||
"\n",
|
||||
"# Representation\n",
|
||||
"\n",
|
||||
"Here's how I will represent Star Battle puzzles:\n",
|
||||
"\n",
|
||||
"- A **cell** is an integer in `range(N * N)`.\n",
|
||||
" - The top row is cells 0, 1, 2, ... left-to-right; the second row is *N*, *N* + 1, *N* + 2, ...; etc.\n",
|
||||
"- A **unit** is a set of cells.\n",
|
||||
"- A **board** is a named tuple with the attributes:\n",
|
||||
" - `N`: the number of cells on each side of the *N*×*N* board.\n",
|
||||
" - `S`: the number of stars per unit in a solution.\n",
|
||||
" - `units`: a list of all the units on the board.\n",
|
||||
" - `units_for`: a dict where `units_for[c]` is a list of the units that cell `c` is in.\n",
|
||||
" - `pic`: a string; a graphical picture of the differently-shaped boxes.\n",
|
||||
"- An intermediate **state** in a search for a solution is a named tuple with the attributes:\n",
|
||||
" - `units`: list of units that have not yet been filled with *S* stars each.\n",
|
||||
" - `stars`: set of cells that have been determined (or guessed) to contain a star.\n",
|
||||
" - `unknowns`: set of cells that might contain either a star or a blank.\n",
|
||||
"- A **solution** is a set of cells where the stars go.\n",
|
||||
"- A **failure** to find a solution is indicated by `None`."
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": null,
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": [
|
||||
"from collections import namedtuple\n",
|
||||
"from functools import lru_cache\n",
|
||||
"from typing import Optional, Iterator, Set, List\n",
|
||||
"\n",
|
||||
"Cell = int\n",
|
||||
"Board = namedtuple('Board', 'N, S, units, units_for, pic')\n",
|
||||
"State = namedtuple('State', 'units, stars, unknowns')"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# Representing Boards\n",
|
||||
"\n",
|
||||
"We can describe the differently-shaped boxes with a **picture** consisting of of *N* lines of *N* non-whitespace characters, where each of *N* distinct characters in the picture corresponds to a box, as in this picture of a 5×5 board with 5 boxes:\n",
|
||||
" \n",
|
||||
" , + ' ' '\n",
|
||||
" , + : : '\n",
|
||||
" , + : : .\n",
|
||||
" , . . . .\n",
|
||||
" , . . . ."
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": null,
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": [
|
||||
"def make_board(S, picture) -> Board:\n",
|
||||
" \"\"\"Create a `Board` from a picture of the boxes.\"\"\"\n",
|
||||
" pic = ''.join(picture.split()) # eliminate whitespace from picture\n",
|
||||
" N = int(len(pic) ** 0.5) # N is √(number of cells)\n",
|
||||
" assert len(pic) == N * N\n",
|
||||
" side = range(0, N)\n",
|
||||
" cols = [{N * r + c for r in side} for c in side]\n",
|
||||
" rows = [{N * r + c for c in side} for r in side]\n",
|
||||
" boxes = [indexes(pic, ch) for ch in set(pic)] \n",
|
||||
" units = cols + rows + boxes\n",
|
||||
" units_for = {c: [u for u in units if c in u]\n",
|
||||
" for c in range(N * N)}\n",
|
||||
" return Board(N, S, units, units_for, pic)\n",
|
||||
"\n",
|
||||
"def indexes(sequence, item) -> Set[int]:\n",
|
||||
" \"\"\"All indexes in sequence where item appears.\"\"\"\n",
|
||||
" return {i for i in range(len(sequence)) if sequence[i] == item}"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"Here's the 5×5 board, and the [board](https://krazydad.com/play/starbattle/?kind=10x10&volumeNumber=1&bookNumber=24&puzzleNumber=18) Barry Hayes shared to introduce me to this type of puzzle, and the \"24\" board. Note that in the \"24\" board the boxes \"2\" and \"t\" form interlocking figure 2s and the boxes \"4\" and \"f\" form interlocking figure 4s."
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": null,
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": [
|
||||
"board5x5 = make_board(1, \"\"\"\n",
|
||||
", + ' ' '\n",
|
||||
", + : : '\n",
|
||||
", + : : .\n",
|
||||
", . . . .\n",
|
||||
", . . . .\n",
|
||||
"\"\"\")\n",
|
||||
"\n",
|
||||
"board1 = make_board(2, \"\"\"\n",
|
||||
"` . . . . . | ; ; ;\n",
|
||||
"` . . . . . | ; ; ;\n",
|
||||
"` ` ` . . . | ; ; ;\n",
|
||||
"` , ` . . . . ; ; ;\n",
|
||||
", , , . . + + = = =\n",
|
||||
", , : : + + + + + +\n",
|
||||
", : : ' ' ' ' ' ' +\n",
|
||||
", : : - - ' ' ' ' '\n",
|
||||
", : : : - - - ' ' '\n",
|
||||
", , , - - - - ' ' '\n",
|
||||
"\"\"\") \n",
|
||||
"\n",
|
||||
"board24 = make_board(2, \"\"\"\n",
|
||||
". . . ' ' , , , , ,\n",
|
||||
". 2 2 2 ' 4 , 4 , -\n",
|
||||
". . . 2 ' 4 , 4 - -\n",
|
||||
". 2 2 2 ' 4 4 4 - -\n",
|
||||
". 2 t t t ; f 4 f -\n",
|
||||
". 2 2 2 t ; f 4 f -\n",
|
||||
". . t t t ; f f f -\n",
|
||||
": : t ; ; ; ; ; f -\n",
|
||||
": : t t t : - ; f -\n",
|
||||
": : : : : : - - - -\n",
|
||||
"\"\"\")"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# Solving Strategy\n",
|
||||
"\n",
|
||||
"I will solve puzzles using **depth-first search** with **constraint propagation**. \n",
|
||||
"\n",
|
||||
"By \"depth-first search\" I mean a procedure that starts from a current state, then creates a new state with a guess that a star should go into some cell *c*, and then tries to solve the rest of the puzzle from the new state. If there is no solution, back up to the old state and guess a different cell for the star. \n",
|
||||
"\n",
|
||||
"By \"constraint propagation\" I mean that whenever a star is placed, check what implications this has for the rest of the board: what blanks and/or stars *must* be placed in what cells. Constraint propagation may be able to prove that the original guess leads to failure, and it may make future guesses easier. \n",
|
||||
"\n",
|
||||
"Note that search always creates a new state for each guess (leaving the old state unaltered so that we can back up to it) and constraint propagation always mutates the state (because the changes are inevitable consequences, not guesses). \n",
|
||||
"\n",
|
||||
"# Constraint Propagation\n",
|
||||
"\n",
|
||||
"The constraint propagation rules are:\n",
|
||||
" \n",
|
||||
"When we **put a star** in a cell:\n",
|
||||
" - Mutate the current state by adding the cell to the set of stars and removing it from the unknowns.\n",
|
||||
" - If any of the cell's units has more than *S* stars, then fail (return `None`).\n",
|
||||
" - Put a blank in each adjacent cell. If you can't, fail.\n",
|
||||
"\n",
|
||||
"When we **put a blank** in a cell:\n",
|
||||
" - Mutate the current state by removing the cell from the unknowns.\n",
|
||||
" - For each of the cell's units:\n",
|
||||
" - If the number of stars plus unknown cells in the unit is less than *S*, then fail.\n",
|
||||
" - If the number equals *S*, then put stars in the unknown cells. If you can't, fail."
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": null,
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": [
|
||||
"def put_star(cell, board, state) -> Optional[State]:\n",
|
||||
" \"\"\"Put a star on the board in the given cell. Mutates state.\n",
|
||||
" Return `None` if it is not possible to place star.\"\"\"\n",
|
||||
" if cell in state.stars:\n",
|
||||
" return state # Already put star in cell\n",
|
||||
" state.unknowns.remove(cell)\n",
|
||||
" state.stars.add(cell)\n",
|
||||
" for unit in board.units_for[cell]:\n",
|
||||
" if count_stars(unit, state) > board.S:\n",
|
||||
" return None\n",
|
||||
" for c in neighbors(cell, board.N):\n",
|
||||
" if c in state.stars or not put_blank(c, board, state):\n",
|
||||
" return None\n",
|
||||
" return state\n",
|
||||
" \n",
|
||||
"def put_blank(cell, board, state) -> Optional[State]:\n",
|
||||
" \"\"\"Put a blank on the board in the given cell. Mutates state.\n",
|
||||
" Return `None` if it is not possible to place blank.\"\"\"\n",
|
||||
" if cell not in state.unknowns:\n",
|
||||
" return state # Already put blank in cell\n",
|
||||
" state.unknowns.remove(cell)\n",
|
||||
" for unit in board.units_for[cell]:\n",
|
||||
" s = count_stars(unit, state)\n",
|
||||
" unknowns = unit & state.unknowns\n",
|
||||
" if s + len(unknowns) < board.S:\n",
|
||||
" return None\n",
|
||||
" if s + len(unknowns) == board.S:\n",
|
||||
" if not all(put_star(c, board, state) for c in unknowns):\n",
|
||||
" return None\n",
|
||||
" return state"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": null,
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": [
|
||||
"def count_stars(unit, state) -> int: return len(unit & state.stars)\n",
|
||||
"\n",
|
||||
"@lru_cache()\n",
|
||||
"def neighbors(cell, N) -> Set[Cell]:\n",
|
||||
" \"\"\"The set of cells that neighbor a given cell on an N×N board.\"\"\"\n",
|
||||
" dxs = {0, +1 if cell % N != N - 1 else 0, -1 if cell % N != 0 else 0}\n",
|
||||
" dys = {0, +N if cell + N < N ** 2 else 0, -N if cell >= N else 0}\n",
|
||||
" return {cell + dx + dy \n",
|
||||
" for dy in dys for dx in dxs if dx or dy}"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# Depth-First Search\n",
|
||||
"\n",
|
||||
"Here are the two more main functions to do search:\n",
|
||||
"1. `solve(board)`: a wrapper function that calls `search` and prints the results.\n",
|
||||
"2. `search(board, state)`: where the real work of searching for a solution is done."
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": null,
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": [
|
||||
"def solve(board) -> Set[Cell]:\n",
|
||||
" \"\"\"Call `search` with an initial state; print board and return solution stars.\n",
|
||||
" Raise an error if there is no solution.\"\"\"\n",
|
||||
" stars = next(search(board, initial_state(board))).stars\n",
|
||||
" print_board(board, stars)\n",
|
||||
" return stars\n",
|
||||
"\n",
|
||||
"def search(board, state) -> Iterator[State]:\n",
|
||||
" \"\"\"Recursive depth-first search for solution(s) to a Star Battle puzzle.\"\"\"\n",
|
||||
" while state.units and count_stars(state.units[0], state) == board.S:\n",
|
||||
" state.units.pop(0) # Discard filled unit(s)\n",
|
||||
" if not state.units: # Succeed\n",
|
||||
" yield state\n",
|
||||
" else: # Guess and recurse\n",
|
||||
" for c in state.units[0] & state.unknowns:\n",
|
||||
" guess_state = put_star(c, board, copy_state(state))\n",
|
||||
" if guess_state is not None:\n",
|
||||
" yield from search(board, guess_state)"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"The inputs to `search` are the static `board` and the dynamic `state` of computation, but what the output should be is less obvious; I considered two choices:\n",
|
||||
"1. `search` returns the first state that represents a solution, or `None` if there is no solution.\n",
|
||||
"2. `search` is a generator that yields all states that represent a solution.\n",
|
||||
"\n",
|
||||
"I decided on the second choice for `search`, even though `solve` only looks at the first solution. That way `search` could be used to verify that puzzles are well-formed, for example.`search` works as follows:\n",
|
||||
" - While the state's first unit is already filled with *S* stars, discard that unit and move on to the next one.\n",
|
||||
" - If the state has no remaining unfilled units, then succeed: yield the state.\n",
|
||||
" - Otherwise, guess and recurse: for each unknown cell *c* in the first unit, create a new state with a star in cell *c*, and if placing the star does not lead to constraint-propagation failure then recursively search from that state.\n",
|
||||
"\n",
|
||||
"Below are the remaining minor functions. *Note:* in `initial_state`, the `units` are `sorted` smallest-unit first, because if, say, a board has *S*=2 and the smallest unit has 3 cells, then you have a 2/3 chance of guessing correctly where the 2 stars should go. With larger units you would be more likely to guess wrong and waste time backing up, so better to do small units first and large units later, when constraint propagation has eliminated some unknown cells."
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": null,
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": [
|
||||
"def copy_state(s: State): return State(s.units[:], set(s.stars), set(s.unknowns))\n",
|
||||
"\n",
|
||||
"def initial_state(board) -> State: \n",
|
||||
" \"\"\"The initial state to start the search for a solution to `board`.\"\"\"\n",
|
||||
" return State(units=sorted(board.units, key=len), \n",
|
||||
" stars=set(), unknowns=set(range(board.N ** 2)))\n",
|
||||
"\n",
|
||||
"def print_board(board, stars) -> None:\n",
|
||||
" \"\"\"Print a representation of the board before and after placing the stars.\n",
|
||||
" The output is not beautiful, but it is readable.\"\"\"\n",
|
||||
" N = board.N\n",
|
||||
" def row(chars, i) -> str: return ' '.join(chars[i * N:(i + 1) * N])\n",
|
||||
" filled = [('*' if c in stars else ch) for c, ch in enumerate(board.pic)]\n",
|
||||
" for i in range(N):\n",
|
||||
" print(row(board.pic, i), ' ' * N, row(filled, i))\n",
|
||||
" print('Valid' if is_solution(board, stars) else 'Invalid', 'solution')\n",
|
||||
" \n",
|
||||
"def is_solution(board, stars) -> bool:\n",
|
||||
" \"\"\"Verify that all units have S stars and that stars are non-adjacent.\"\"\"\n",
|
||||
" return (all(len(stars & unit) == board.S\n",
|
||||
" for unit in board.units) and\n",
|
||||
" all(c1 not in neighbors(c2, board.N)\n",
|
||||
" for c1 in stars for c2 in stars))"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# Solutions\n"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": null,
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": [
|
||||
"solve(board5x5)"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": 9,
|
||||
"metadata": {},
|
||||
"outputs": [
|
||||
{
|
||||
"name": "stdout",
|
||||
"output_type": "stream",
|
||||
"text": [
|
||||
"` . . . . . | ; ; ; ` . . . . . * ; * ;\n",
|
||||
"` . . . . . | ; ; ; ` * . . * . | ; ; ;\n",
|
||||
"` ` ` . . . | ; ; ; ` ` ` . . . * ; * ;\n",
|
||||
"` , ` . . . . ; ; ; * , * . . . . ; ; ;\n",
|
||||
", , , . . + + = = = , , , . . + + * = *\n",
|
||||
", , : : + + + + + + , , : * + * + + + +\n",
|
||||
", : : ' ' ' ' ' ' + , * : ' ' ' ' ' ' *\n",
|
||||
", : : - - ' ' ' ' ' , : : * - * ' ' ' '\n",
|
||||
", : : : - - - ' ' ' * : : : - - - * ' '\n",
|
||||
", , , - - - - ' ' ' , , * - * - - ' ' '\n",
|
||||
"Valid solution\n"
|
||||
]
|
||||
},
|
||||
{
|
||||
"data": {
|
||||
"text/plain": [
|
||||
"{6, 8, 11, 14, 26, 28, 30, 32, 47, 49, 53, 55, 61, 69, 73, 75, 80, 87, 92, 94}"
|
||||
]
|
||||
},
|
||||
"execution_count": 9,
|
||||
"metadata": {},
|
||||
"output_type": "execute_result"
|
||||
}
|
||||
],
|
||||
"source": [
|
||||
"solve(board1)"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": 10,
|
||||
"metadata": {},
|
||||
"outputs": [
|
||||
{
|
||||
"name": "stdout",
|
||||
"output_type": "stream",
|
||||
"text": [
|
||||
". . . ' ' , , , , , . . . ' ' , * , , *\n",
|
||||
". 2 2 2 ' 4 , 4 , - . 2 * 2 * 4 , 4 , -\n",
|
||||
". . . 2 ' 4 , 4 - - * . . 2 ' 4 , * - -\n",
|
||||
". 2 2 2 ' 4 4 4 - - . 2 * 2 * 4 4 4 - -\n",
|
||||
". 2 t t t ; f 4 f - . 2 t t t ; f * f *\n",
|
||||
". 2 2 2 t ; f 4 f - * 2 2 2 t * f 4 f -\n",
|
||||
". . t t t ; f f f - . . t * t ; f f * -\n",
|
||||
": : t ; ; ; ; ; f - : * t ; ; * ; ; f -\n",
|
||||
": : t t t : - ; f - : : t * t : - ; * -\n",
|
||||
": : : : : : - - - - : * : : : : * - - -\n",
|
||||
"Valid solution\n"
|
||||
]
|
||||
},
|
||||
{
|
||||
"data": {
|
||||
"text/plain": [
|
||||
"{6, 9, 12, 14, 20, 27, 32, 34, 47, 49, 50, 55, 63, 68, 71, 75, 83, 88, 91, 96}"
|
||||
]
|
||||
},
|
||||
"execution_count": 10,
|
||||
"metadata": {},
|
||||
"output_type": "execute_result"
|
||||
}
|
||||
],
|
||||
"source": [
|
||||
"solve(board24)"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": 11,
|
||||
"metadata": {},
|
||||
"outputs": [
|
||||
{
|
||||
"name": "stdout",
|
||||
"output_type": "stream",
|
||||
"text": [
|
||||
"CPU times: user 195 ms, sys: 2.98 ms, total: 198 ms\n",
|
||||
"Wall time: 197 ms\n"
|
||||
]
|
||||
}
|
||||
],
|
||||
"source": [
|
||||
"%%time\n",
|
||||
"for board in (board5x5, board1, board24):\n",
|
||||
" assert next(search(board, initial_state(board))).stars"
|
||||
]
|
||||
}
|
||||
],
|
||||
"metadata": {
|
||||
"kernelspec": {
|
||||
"display_name": "Python 3",
|
||||
"language": "python",
|
||||
"name": "python3"
|
||||
},
|
||||
"language_info": {
|
||||
"codemirror_mode": {
|
||||
"name": "ipython",
|
||||
"version": 3
|
||||
},
|
||||
"file_extension": ".py",
|
||||
"mimetype": "text/x-python",
|
||||
"name": "python",
|
||||
"nbconvert_exporter": "python",
|
||||
"pygments_lexer": "ipython3",
|
||||
"version": "3.7.6"
|
||||
}
|
||||
},
|
||||
"nbformat": 4,
|
||||
"nbformat_minor": 4
|
||||
}
|
||||
BIN
ipynb/Sudoku$1.class
Normal file
BIN
ipynb/Sudoku$1.class
Normal file
Binary file not shown.
BIN
ipynb/Sudoku$2.class
Normal file
BIN
ipynb/Sudoku$2.class
Normal file
Binary file not shown.
BIN
ipynb/Sudoku.class
Normal file
BIN
ipynb/Sudoku.class
Normal file
Binary file not shown.
1017
ipynb/Sudoku.ipynb
Normal file
1017
ipynb/Sudoku.ipynb
Normal file
File diff suppressed because it is too large
Load Diff
488
ipynb/Sudoku.java
Normal file
488
ipynb/Sudoku.java
Normal file
@ -0,0 +1,488 @@
|
||||
import java.io.*;
|
||||
import java.lang.Integer.*;
|
||||
import java.util.*;
|
||||
import java.util.stream.*;
|
||||
import java.lang.StringBuilder;
|
||||
import java.util.concurrent.CountDownLatch;
|
||||
|
||||
//////////////////////////////// Solve Sudoku Puzzles ////////////////////////////////
|
||||
//////////////////////////////// @author Peter Norvig ////////////////////////////////
|
||||
|
||||
/** There are two representations of puzzles that we will use:
|
||||
** 1. A gridstring is 81 chars, with characters '0' or '.' for blank and '1' to '9' for digits.
|
||||
** 2. A puzzle grid is an int[81] with a digit d (1-9) represented by the integer (1 << (d - 1));
|
||||
** that is, a bit pattern that has a single 1 bit representing the digit.
|
||||
** A blank is represented by the OR of all the digits 1-9, meaning that any digit is possible.
|
||||
** While solving the puzzle, some of these digits are eliminated, leaving fewer possibilities.
|
||||
** The puzzle is solved when every square has only a single possibility.
|
||||
**
|
||||
** Search for a solution with `search`:
|
||||
** - Fill an empty square with a guessed digit and do constraint propagation.
|
||||
** - If the guess is consistent, search deeper; if not, try a different guess for the square.
|
||||
** - If all guesses fail, back up to the previous level.
|
||||
** - In selecting an empty square, we pick one that has the minimum number of possible digits.
|
||||
** - To be able to back up, we need to keep the grid from the previous recursive level.
|
||||
** But we only need to keep one grid for each level, so to save garbage collection,
|
||||
** we pre-allocate one grid per level (there are 81 levels) in a `gridpool`.
|
||||
** Do constraint propagation with `arcConsistent`, `dualConsistent`, and `nakedPairs`.
|
||||
**/
|
||||
|
||||
public class Sudoku {
|
||||
|
||||
//////////////////////////////// main; command line options //////////////////////////////
|
||||
|
||||
static final String usage = String.join("\n",
|
||||
"usage: java Sudoku -(no)[fghnprstuv] | -[RT]<number> | <filename> ...",
|
||||
"E.g., -v turns verify flag on, -nov turns it off. -R and -T require a number. The options:\n",
|
||||
" -f(ile) Print summary stats for each file (default on)",
|
||||
" -g(rid) Print each puzzle grid and solution grid (default off)",
|
||||
" -h(elp) Print this usage message",
|
||||
" -n(aked) Run naked pairs (default on)",
|
||||
" -p(uzzle) Print summary stats for each puzzle (default off)",
|
||||
" -r(everse) Solve the reverse of each puzzle as well as each puzzle itself (default off)",
|
||||
" -s(earch) Run search (default on, but some puzzles can be solved with CSP methods alone)",
|
||||
" -t(hread) Print summary stats for each thread (default off)",
|
||||
" -u(nitTest)Run a suite of unit tests (default off)",
|
||||
" -v(erify) Verify each solution is valid (default on)",
|
||||
" -T<number> Concurrently run <number> threads (default 26)",
|
||||
" -R<number> Repeat each puzzle <number> times (default 1)",
|
||||
" <filename> Solve all puzzles in filename, which has one puzzle per line");
|
||||
|
||||
boolean printFileStats = true; // -f
|
||||
boolean printGrid = false; // -g
|
||||
boolean runNakedPairs = true; // -n
|
||||
boolean printPuzzleStats = false; // -p
|
||||
boolean reversePuzzle = false; // -r
|
||||
boolean runSearch = true; // -s
|
||||
boolean printThreadStats = false; // -t
|
||||
boolean verifySolution = true; // -v
|
||||
int nThreads = 26; // -T
|
||||
int repeat = 1; // -R
|
||||
|
||||
int backtracks = 0; // count total backtracks
|
||||
|
||||
/** Parse command line args and solve puzzles in files. **/
|
||||
public static void main(String[] args) throws IOException {
|
||||
Sudoku s = new Sudoku();
|
||||
for (String arg: args) {
|
||||
if (!arg.startsWith("-")) {
|
||||
s.solveFile(arg);
|
||||
} else {
|
||||
boolean value = !arg.startsWith("-no");
|
||||
switch(arg.charAt(value ? 1 : 3)) {
|
||||
case 'f': s.printFileStats = value; break;
|
||||
case 'g': s.printGrid = value; break;
|
||||
case 'h': System.out.println(usage); break;
|
||||
case 'n': s.runNakedPairs = value; break;
|
||||
case 'p': s.printPuzzleStats = value; break;
|
||||
case 'r': s.reversePuzzle = value; break;
|
||||
case 's': s.runSearch = value; break;
|
||||
case 't': s.printThreadStats = value; break;
|
||||
case 'u': s.runUnitTests(); break;
|
||||
case 'v': s.verifySolution = value; break;
|
||||
case 'T': s.nThreads = Integer.parseInt(arg.substring(2)); break;
|
||||
case 'R': s.repeat = Integer.parseInt(arg.substring(2)); break;
|
||||
default: System.out.println("Unrecognized option: " + arg + "\n" + usage);
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
//////////////////////////////// Handling Lists of Puzzles ////////////////////////////////
|
||||
|
||||
/** Solve all the puzzles in a file. Report timing statistics. **/
|
||||
void solveFile(String filename) throws IOException {
|
||||
List<int[]> grids = readFile(filename);
|
||||
long startFileTime = System.nanoTime();
|
||||
switch(nThreads) {
|
||||
case 1: solveList(grids); break;
|
||||
default: solveListThreaded(grids, nThreads); break;
|
||||
}
|
||||
if (printFileStats) printStats(grids.size() * repeat, startFileTime, filename);
|
||||
}
|
||||
|
||||
|
||||
/** Solve a list of puzzles in a single thread.
|
||||
** repeat -R<number> times; print each puzzle's stats if -p; print grid if -g; verify if -v. **/
|
||||
void solveList(List<int[]> grids) {
|
||||
int[] puzzle = new int[N * N]; // Used to save a copy of the original grid
|
||||
int[][] gridpool = new int[N * N][N * N]; // Reuse grids during the search
|
||||
for (int g=0; g<grids.size(); ++g) {
|
||||
int grid[] = grids.get(g);
|
||||
System.arraycopy(grid, 0, puzzle, 0, grid.length);
|
||||
for (int i = 0; i < repeat; ++i) {
|
||||
long startTime = printPuzzleStats ? System.nanoTime() : 0;
|
||||
int[] solution = initialize(grid); // All the real work is
|
||||
if (runSearch) solution = search(solution, gridpool, 0); // on these 2 lines.
|
||||
if (printPuzzleStats) {
|
||||
printStats(1, startTime, "Puzzle " + (g + 1));
|
||||
}
|
||||
if (i == 0 && (printGrid || (verifySolution && !verify(solution, puzzle)))) {
|
||||
printGrids("Puzzle " + (g + 1), grid, solution);
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
/** Break a list of puzzles into nThreads sublists and solve each sublist in a separate thread. **/
|
||||
void solveListThreaded(List<int[]> grids, int nThreads) {
|
||||
try {
|
||||
final long startTime = System.nanoTime();
|
||||
int nGrids = grids.size();
|
||||
final CountDownLatch latch = new CountDownLatch(nThreads);
|
||||
int size = nGrids / nThreads;
|
||||
for (int c = 0; c < nThreads; ++c) {
|
||||
int end = c == nThreads - 1 ? nGrids : (c + 1) * size;
|
||||
final List<int[]> sublist = grids.subList(c * size, end);
|
||||
new Thread() {
|
||||
public void run() {
|
||||
solveList(sublist);
|
||||
latch.countDown();
|
||||
if (printThreadStats) {
|
||||
printStats(repeat * sublist.size(), startTime, "Thread");
|
||||
}
|
||||
}
|
||||
}.start();
|
||||
}
|
||||
latch.await(); // Wait for all threads to finish
|
||||
} catch (InterruptedException e) {
|
||||
System.err.println("And you may ask yourself, 'Well, how did I get here?'");
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
//////////////////////////////// Utility functions ////////////////////////////////
|
||||
|
||||
/** Return an array of all squares in the intersection of these rows and cols **/
|
||||
int[] cross(int[] rows, int[] cols) {
|
||||
int[] result = new int[rows.length * cols.length];
|
||||
int i = 0;
|
||||
for (int r: rows) { for (int c: cols) { result[i++] = N * r + c; } }
|
||||
return result;
|
||||
}
|
||||
|
||||
|
||||
/** Return true iff item is an element of array, or of array[0:end]. **/
|
||||
boolean member(int item, int[] array) { return member(item, array, array.length); }
|
||||
boolean member(int item, int[] array, int end) {
|
||||
for (int i = 0; i<end; ++i) {
|
||||
if (array[i] == item) { return true; }
|
||||
}
|
||||
return false;
|
||||
}
|
||||
|
||||
|
||||
//////////////////////////////// Constants ////////////////////////////////
|
||||
|
||||
final int N = 9; // Number of cells on a side of grid.
|
||||
final int[] DIGITS = {1<<0, 1<<1, 1<<2, 1<<3, 1<<4, 1<<5, 1<<6, 1<<7, 1<<8};
|
||||
final int ALL_DIGITS = Integer.parseInt("111111111", 2);
|
||||
final int[] ROWS = IntStream.range(0, N).toArray();
|
||||
final int[] COLS = ROWS;
|
||||
final int[] SQUARES = IntStream.range(0, N * N).toArray();
|
||||
final int[][] BLOCKS = {{0, 1, 2}, {3, 4, 5}, {6, 7, 8}};
|
||||
final int[][] ALL_UNITS = new int[3 * N][];
|
||||
final int[][][] UNITS = new int[N * N][3][N];
|
||||
final int[][] PEERS = new int[N * N][20];
|
||||
final int[] NUM_DIGITS = new int[ALL_DIGITS + 1];
|
||||
final int[] HIGHEST_DIGIT = new int[ALL_DIGITS + 1];
|
||||
|
||||
{
|
||||
// Initialize ALL_UNITS to be an array of the 27 units: rows, columns, and blocks
|
||||
int i = 0;
|
||||
for (int r: ROWS) {ALL_UNITS[i++] = cross(new int[] {r}, COLS); }
|
||||
for (int c: COLS) {ALL_UNITS[i++] = cross(ROWS, new int[] {c}); }
|
||||
for (int[] rb: BLOCKS) {for (int[] cb: BLOCKS) {ALL_UNITS[i++] = cross(rb, cb); } }
|
||||
|
||||
// Initialize each UNITS[s] to be an array of the 3 units for square s.
|
||||
for (int s: SQUARES) {
|
||||
i = 0;
|
||||
for (int[] u: ALL_UNITS) {
|
||||
if (member(s, u)) UNITS[s][i++] = u;
|
||||
}
|
||||
}
|
||||
|
||||
// Initialize each PEERS[s] to be an array of the 20 squares that are peers of square s.
|
||||
for (int s: SQUARES) {
|
||||
i = 0;
|
||||
for (int[] u: UNITS[s]) {
|
||||
for (int s2: u) {
|
||||
if (s2 != s && !member(s2, PEERS[s], i)) {
|
||||
PEERS[s][i++] = s2;
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
// Initialize NUM_DIGITS[val] to be the number of 1 bits in the bitset val
|
||||
// and HIGHEST_DIGIT[val] to the highest bit set in the bitset val
|
||||
for (int val = 0; val <= ALL_DIGITS; val++) {
|
||||
NUM_DIGITS[val] = Integer.bitCount(val);
|
||||
HIGHEST_DIGIT[val] = Integer.highestOneBit(val);
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
//////////////////////////////// Search algorithm ////////////////////////////////
|
||||
|
||||
/** Search for a solution to grid. If there is an unfilled square, select one
|
||||
** and try--that is, search recursively--every possible digit for the square. **/
|
||||
int[] search(int[] grid, int[][] gridpool, int level) {
|
||||
if (grid == null) {
|
||||
return null;
|
||||
}
|
||||
int s = select_square(grid);
|
||||
if (s == -1) {
|
||||
return grid; // No squares to select means we are done!
|
||||
}
|
||||
for (int d: DIGITS) {
|
||||
// For each possible digit d that could fill square s, try it
|
||||
if ((d & grid[s]) > 0) {
|
||||
// Copy grid's contents into gridpool[level], and use that at the next level
|
||||
System.arraycopy(grid, 0, gridpool[level], 0, grid.length);
|
||||
int[] result = search(fill(gridpool[level], s, d), gridpool, level + 1);
|
||||
if (result != null) {
|
||||
return result;
|
||||
}
|
||||
backtracks += 1;
|
||||
}
|
||||
}
|
||||
return null;
|
||||
}
|
||||
|
||||
|
||||
/** Verify that grid is a solution to the puzzle. **/
|
||||
boolean verify(int[] grid, int[] puzzle) {
|
||||
if (grid == null) { return false; }
|
||||
// Check that all squares have a single digit, and
|
||||
// no filled square in the puzzle was changed in the solution.
|
||||
for (int s: SQUARES) {
|
||||
if ((NUM_DIGITS[grid[s]] != 1) || (NUM_DIGITS[puzzle[s]] == 1 && grid[s] != puzzle[s])) {
|
||||
return false;
|
||||
}
|
||||
}
|
||||
// Check that each unit is a permutation of digits
|
||||
for (int[] u: ALL_UNITS) {
|
||||
int unit_digits = 0; // All the digits in a unit.
|
||||
for (int s : u) {unit_digits |= grid[s]; }
|
||||
if (unit_digits != ALL_DIGITS) {
|
||||
return false;
|
||||
}
|
||||
}
|
||||
return true;
|
||||
}
|
||||
|
||||
|
||||
/** Choose an unfilled square with the minimum number of possible values.
|
||||
** If all squares are filled, return -1 (which means the puzzle is complete). **/
|
||||
int select_square(int[] grid) {
|
||||
int square = -1;
|
||||
int min = N + 1;
|
||||
for (int s: SQUARES) {
|
||||
int c = NUM_DIGITS[grid[s]];
|
||||
if (c == 2) {
|
||||
return s; // Can't get fewer than 2 possible digits
|
||||
} else if (c > 1 && c < min) {
|
||||
square = s;
|
||||
min = c;
|
||||
}
|
||||
}
|
||||
return square;
|
||||
}
|
||||
|
||||
|
||||
/** fill grid[s] = d. If this leads to contradiction, return null. **/
|
||||
int[] fill(int[] grid, int s, int d) {
|
||||
if ((grid == null) || ((grid[s] & d) == 0)) { return null; } // d not possible for grid[s]
|
||||
grid[s] = d;
|
||||
for (int p: PEERS[s]) {
|
||||
if (!eliminate(grid, p, d)) { // If we can't eliminate d from all peers of s, then fail
|
||||
return null;
|
||||
}
|
||||
}
|
||||
return grid;
|
||||
}
|
||||
|
||||
|
||||
/** Eliminate digit d as a possibility for grid[s].
|
||||
** Run the 3 constraint propagation routines.
|
||||
** If constraint propagation detects a contradiction, return false. **/
|
||||
boolean eliminate(int[] grid, int s, int d) {
|
||||
if ((grid[s] & d) == 0) { return true; } // d already eliminated from grid[s]
|
||||
grid[s] -= d;
|
||||
return arc_consistent(grid, s) && dual_consistent(grid, s, d) && naked_pairs(grid, s);
|
||||
}
|
||||
|
||||
|
||||
//////////////////////////////// Constraint Propagation ////////////////////////////////
|
||||
|
||||
/** Check if square s is consistent: that is, it has multiple possible values, or it has
|
||||
** one possible value which we can consistently fill. **/
|
||||
boolean arc_consistent(int[] grid, int s) {
|
||||
int count = NUM_DIGITS[grid[s]];
|
||||
return count >= 2 || (count == 1 && (fill(grid, s, grid[s]) != null));
|
||||
}
|
||||
|
||||
|
||||
/** After we eliminate d from possibilities for grid[s], check each unit of s
|
||||
** and make sure there is some position in the unit where d can go.
|
||||
** If there is only one possible place for d, fill it with d. **/
|
||||
boolean dual_consistent(int[] grid, int s, int d) {
|
||||
for (int[] u: UNITS[s]) {
|
||||
int dPlaces = 0; // The number of possible places for d within unit u
|
||||
int dplace = -1; // Try to find a place in the unit where d can go
|
||||
for (int s2: u) {
|
||||
if ((grid[s2] & d) > 0) { // s2 is a possible place for d
|
||||
dPlaces++;
|
||||
if (dPlaces > 1) break;
|
||||
dplace = s2;
|
||||
}
|
||||
}
|
||||
if (dPlaces == 0 || (dPlaces == 1 && (fill(grid, dplace, d) == null))) {
|
||||
return false;
|
||||
}
|
||||
}
|
||||
return true;
|
||||
}
|
||||
|
||||
|
||||
/** Look for two squares in a unit with the same two possible values, and no other values.
|
||||
** For example, if s and s2 both have the possible values 8|9, then we know that 8 and 9
|
||||
** must go in those two squares. We don't know which is which, but we can eliminate
|
||||
** 8 and 9 from any other square s3 that is in the unit. **/
|
||||
boolean naked_pairs(int[] grid, int s) {
|
||||
if (!runNakedPairs) { return true; }
|
||||
int val = grid[s];
|
||||
if (NUM_DIGITS[val] != 2) { return true; } // Doesn't apply
|
||||
for (int s2: PEERS[s]) {
|
||||
if (grid[s2] == val) {
|
||||
// s and s2 are a naked pair; find what unit(s) they share
|
||||
for (int[] u: UNITS[s]) {
|
||||
if (member(s2, u)) {
|
||||
for (int s3: u) { // s3 can't have either of the values in val (e.g. 8|9)
|
||||
if (s3 != s && s3 != s2) {
|
||||
int d = HIGHEST_DIGIT[val];
|
||||
int d2 = val - d;
|
||||
if (!eliminate(grid, s3, d) || !eliminate(grid, s3, d2)) {
|
||||
return false;
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
return true;
|
||||
}
|
||||
|
||||
|
||||
//////////////////////////////// Input ////////////////////////////////
|
||||
|
||||
/** The method `readFile` reads one puzzle per file line and returns a List of puzzle grids. **/
|
||||
List<int[]> readFile(String filename) throws IOException {
|
||||
BufferedReader in = new BufferedReader(new FileReader(filename));
|
||||
List<int[]> grids = new ArrayList<int[]>(1000);
|
||||
String gridstring;
|
||||
while ((gridstring = in.readLine()) != null) {
|
||||
grids.add(parseGrid(gridstring));
|
||||
if (reversePuzzle) {
|
||||
grids.add(parseGrid(new StringBuilder(gridstring).reverse().toString()));
|
||||
}
|
||||
}
|
||||
return grids;
|
||||
}
|
||||
|
||||
|
||||
/** Parse a gridstring into a puzzle grid: an int[] with values DIGITS[0-9] or ALL_DIGITS. **/
|
||||
int[] parseGrid(String gridstring) {
|
||||
int[] grid = new int[N * N];
|
||||
int s = 0;
|
||||
for (int i = 0; i<gridstring.length(); ++i) {
|
||||
char c = gridstring.charAt(i);
|
||||
if ('1' <= c && c <= '9') {
|
||||
grid[s++] = DIGITS[c - '1']; // A single-bit set to represent a digit
|
||||
} else if (c == '0' || c == '.') {
|
||||
grid[s++] = ALL_DIGITS; // Any digit is possible
|
||||
}
|
||||
}
|
||||
assert s == N * N;
|
||||
return grid;
|
||||
}
|
||||
|
||||
|
||||
/** Initialize a grid from a puzzle.
|
||||
** First initialize every square in the new grid to ALL_DIGITS, meaning any value is possible.
|
||||
** Then, call `fill` on the puzzle's filled squares to initiate constraint propagation. **/
|
||||
int[] initialize(int[] puzzle) {
|
||||
int[] grid = new int[N * N]; Arrays.fill(grid, ALL_DIGITS);
|
||||
for (int s: SQUARES) { if (puzzle[s] != ALL_DIGITS) { fill(grid, s, puzzle[s]); } }
|
||||
return grid;
|
||||
}
|
||||
|
||||
|
||||
//////////////////////////////// Output and Tests ////////////////////////////////
|
||||
|
||||
boolean headerPrinted = false;
|
||||
|
||||
/** Print stats on puzzles solved, average time, frequency, threads used, and name. **/
|
||||
void printStats(int nGrids, long startTime, String name) {
|
||||
double usecs = (System.nanoTime() - startTime) / 1000.;
|
||||
String line = String.format("%7d %6.1f %7.3f %7d %10.1f %s",
|
||||
nGrids, usecs / nGrids, 1000 * nGrids / usecs, nThreads, backtracks * 1. / nGrids, name);
|
||||
synchronized (this) { // So that printing from different threads doesn't get garbled
|
||||
if (!headerPrinted) {
|
||||
System.out.println("Puzzles μsec KHz Threads Backtracks Name\n"
|
||||
+ "======= ====== ======= ======= ========== ====");
|
||||
headerPrinted = true;
|
||||
}
|
||||
System.out.println(line);
|
||||
backtracks = 0;
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
/** Print the original puzzle grid and the solution grid. **/
|
||||
void printGrids(String name, int[] puzzle, int[] solution) {
|
||||
String bar = "------+-------+------";
|
||||
String gap = " "; // Space between the puzzle grid and solution grid
|
||||
if (solution == null) solution = new int[N * N];
|
||||
synchronized (this) { // So that printing from different threads doesn't get garbled
|
||||
System.out.format("\n%-22s%s%s\n", name + ":", gap,
|
||||
(verify(solution, puzzle) ? "Solution:" : "FAILED:"));
|
||||
for (int r = 0; r < N; ++r) {
|
||||
System.out.println(rowString(puzzle, r) + gap + rowString(solution, r));
|
||||
if (r == 2 || r == 5) System.out.println(bar + gap + " " + bar);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
/** Return a String representing a row of this puzzle. **/
|
||||
String rowString(int[] grid, int r) {
|
||||
String row = "";
|
||||
for (int s = r * 9; s < (r + 1) * 9; ++s) {
|
||||
row += (char) ((NUM_DIGITS[grid[s]] == 9) ? '.' : (NUM_DIGITS[grid[s]] != 1) ? '?' :
|
||||
('1' + Integer.numberOfTrailingZeros(grid[s])));
|
||||
row += (s % 9 == 2 || s % 9 == 5 ? " | " : " ");
|
||||
}
|
||||
return row;
|
||||
}
|
||||
|
||||
|
||||
/** Unit Tests. Just getting started with these. **/
|
||||
void runUnitTests() {
|
||||
assert N == 9;
|
||||
assert SQUARES.length == 81;
|
||||
for (int s: SQUARES) {
|
||||
assert UNITS[s].length == 3;
|
||||
assert PEERS[s].length == 20;
|
||||
}
|
||||
assert Arrays.equals(PEERS[19],
|
||||
new int[] {18, 20, 21, 22, 23, 24, 25, 26, 1, 10, 28, 37, 46, 55, 64, 73, 0, 2, 9, 11});
|
||||
assert Arrays.deepToString(UNITS[19]).equals(
|
||||
"[[18, 19, 20, 21, 22, 23, 24, 25, 26], [1, 10, 19, 28, 37, 46, 55, 64, 73], [0, 1, 2, 9, 10, 11, 18, 19, 20]]");
|
||||
System.out.println("Unit tests pass.");
|
||||
}
|
||||
}
|
||||
1355
ipynb/SudokuJava.ipynb
Normal file
1355
ipynb/SudokuJava.ipynb
Normal file
File diff suppressed because one or more lines are too long
10
ipynb/hardest.txt
Normal file
10
ipynb/hardest.txt
Normal file
@ -0,0 +1,10 @@
|
||||
85...24..72......9..4.........1.7..23.5...9...4...........8..7..17..........36.4.
|
||||
..53.....8......2..7..1.5..4....53...1..7...6..32...8..6.5....9..4....3......97..
|
||||
12..4......5.69.1...9...5.........7.7...52.9..3......2.9.6...5.4..9..8.1..3...9.4
|
||||
...57..3.1......2.7...234......8...4..7..4...49....6.5.42...3.....7..9....18.....
|
||||
1....7.9..3..2...8..96..5....53..9...1..8...26....4...3......1..4......7..7...3..
|
||||
1...34.8....8..5....4.6..21.18......3..1.2..6......81.52..7.9....6..9....9.64...2
|
||||
...92......68.3...19..7...623..4.1....1...7....8.3..297...8..91...5.72......64...
|
||||
.6.5.4.3.1...9...8.........9...5...6.4.6.2.7.7...4...5.........4...8...1.5.2.3.4.
|
||||
7.....4...2..7..8...3..8.799..5..3...6..2..9...1.97..6...3..9...3..4..6...9..1.35
|
||||
....7..2.8.......6.1.2.5...9.54....8.........3....85.1...3.2.8.4.......9.7..6....
|
||||
1
ipynb/one.txt
Normal file
1
ipynb/one.txt
Normal file
@ -0,0 +1 @@
|
||||
..7........1....3..5..4.6...4....7...6...3........1..2.....7.......6..8...2.....1
|
||||
500000
ipynb/sudata.txt
Normal file
500000
ipynb/sudata.txt
Normal file
File diff suppressed because it is too large
Load Diff
10000
ipynb/sudoku10k.txt
Normal file
10000
ipynb/sudoku10k.txt
Normal file
File diff suppressed because it is too large
Load Diff
10
ipynb/ten.txt
Normal file
10
ipynb/ten.txt
Normal file
@ -0,0 +1,10 @@
|
||||
..7........1....3..5..4.6...4....7...6...3........1..2.....7.......6..8...2.....1
|
||||
..3..2.8.14......9.68.593.7..24.5...............2.85..9.457.86.6......75.8.6..4..
|
||||
.....4.....5.....3...8.1.6.......81..73........2..6.......2....14...........5...7
|
||||
......8..3...6.9.71.8.9..6..673...2....2.6....2...938..3..8.1.25.267...8..9......
|
||||
......7.4.1.5......6..........15.9..8.....3.....6.....4...97.....7..8..........1.
|
||||
..2..6..7......8.9.8..4..6.85.2..93.....3.....93..1.25.1..9..5.5.4......2..3..6..
|
||||
.....8......6.4.........1.7....9......5.....36......84..7.......4.....6.....269..
|
||||
....1......4....6....85............289............7.34.........15....8....3..4..7
|
||||
...9.........1..7..9...4.2..4.16.....5.3......1...7.533......1....58..4.8.....2..
|
||||
.......8...4....15..23.7........3...8.......1.....2..6........4....1.....26...7..
|
||||
48697
ipynb/usecs.txt
Normal file
48697
ipynb/usecs.txt
Normal file
File diff suppressed because it is too large
Load Diff
Loading…
Reference in New Issue
Block a user