# Sorting-Algorithms-Blender

## Bubble Sort

![bubble](https://user-images.githubusercontent.com/78089013/167689895-ba7e3ddd-6ea9-41e0-8767-0700b12b6664.gif)

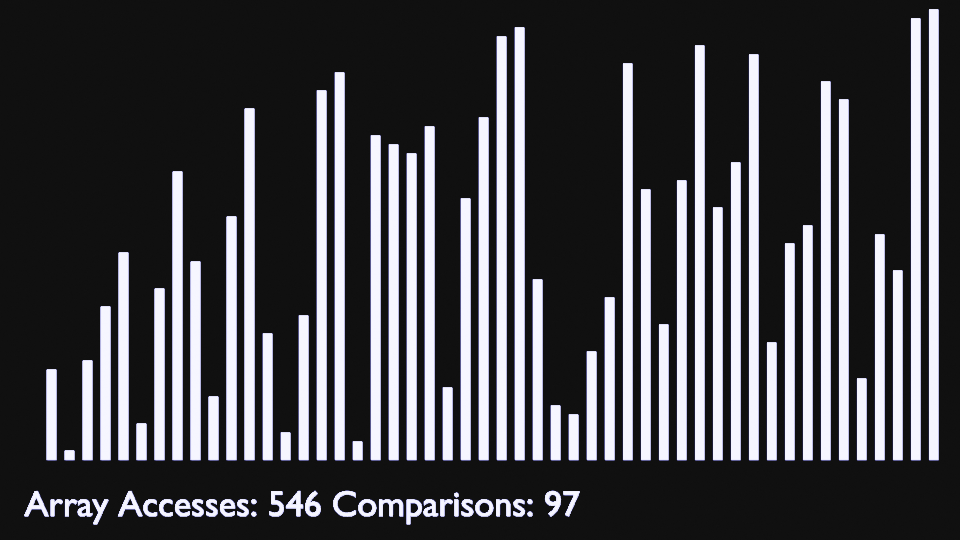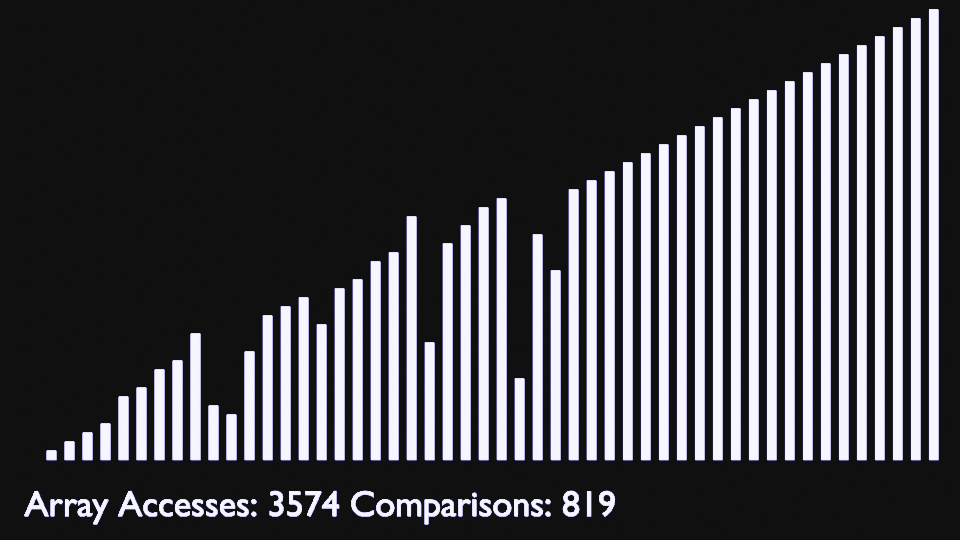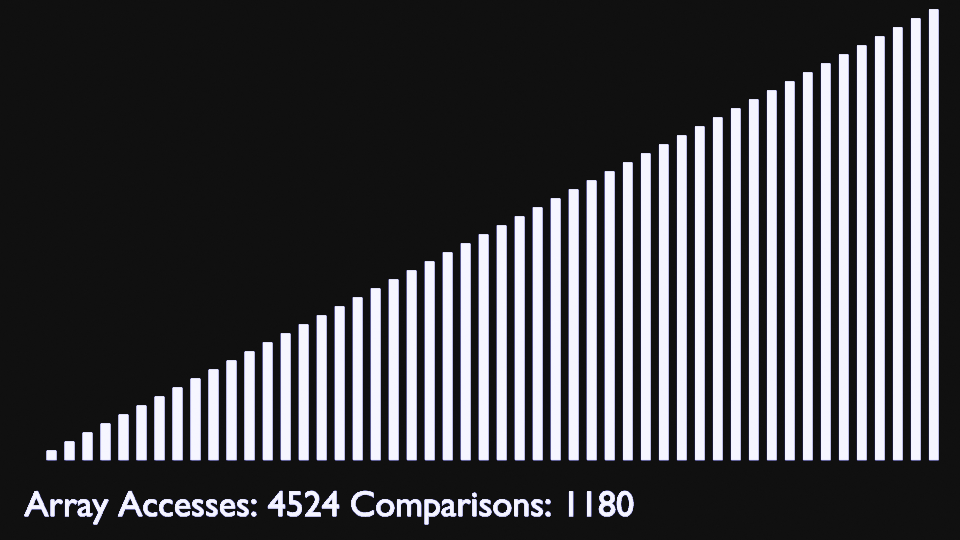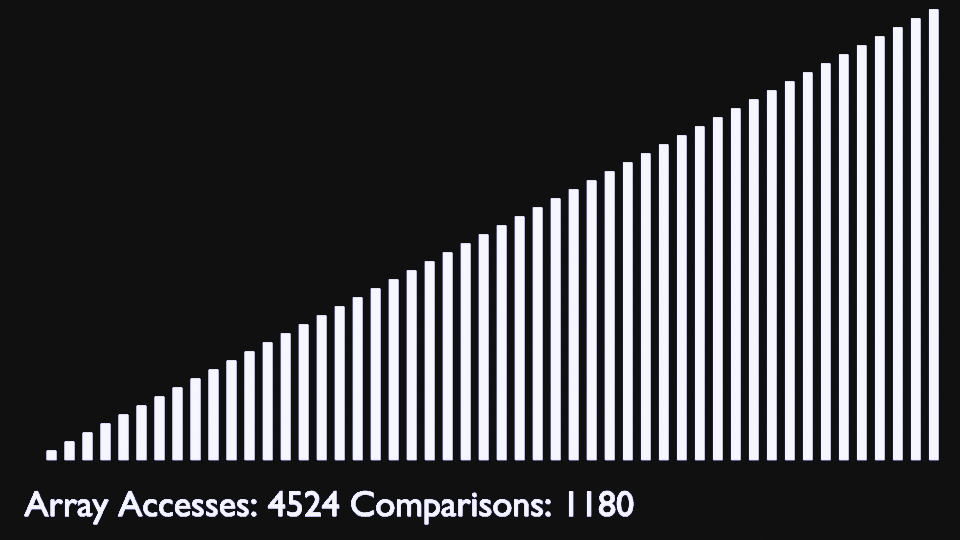
## Insertion Sort

![Inerstio](https://user-images.githubusercontent.com/78089013/170041841-1c114899-1ada-4278-9865-6939774f373f.gif)

## Big O

<table>
    <tr>
      <th>Algorithm</th>
      <th colspan="3">Time Complexity</th>
      <th>Space Complexity</th>
    </tr>
    <tr>
      <th></th>
      <th>Best</th>
      <th>Average</th>
      <th>Worst</th>
      <th>Worst</th>
    </tr>
    <tr>
      <td><a href="http://en.wikipedia.org/wiki/Quicksort">Quicksort</a></td>
      <td><code class="orange">
        Ω(n log(n))</code>
      </td>
      <td><code class="orange">Θ(n log(n))</code></td>
      <td><code class="orange">O(n^2)</code></td>
      <td><code class="orange">O(log(n))</code></td>
    </tr>
    <tr>
      <td><a href="http://en.wikipedia.org/wiki/Merge_sort">Mergesort</a></td>
      <td><code class="orange">Ω(n log(n))</code></td>
      <td><code class="orange">Θ(n log(n))</code></td>
      <td><code class="orange">O(n log(n))</code></td>
      <td><code class="yellow">O(n)</code></td>
    </tr>
    <tr>
      <td><a href="http://en.wikipedia.org/wiki/Timsort">Timsort</a></td>
      <td><code class="yellow">Ω(n)</code></td>
      <td><code class="orange">Θ(n log(n))</code></td>
      <td><code class="orange">O(n log(n))</code></td>
      <td><code class="yellow">O(n)</code></td>
    </tr>
    <tr>
      <td><a href="http://en.wikipedia.org/wiki/Heapsort">Heapsort</a></td>
      <td><code class="orange">Ω(n log(n))</code></td>
      <td><code class="orange">Θ(n log(n))</code></td>
      <td><code class="orange">O(n log(n))</code></td>
      <td><code class="green">O(1)</code></td>
    </tr>
    <tr>
      <td><a href="http://en.wikipedia.org/wiki/Bubble_sort">Bubble Sort</a></td>
      <td><code class="yellow">Ω(n)</code></td>
      <td><code class="red">Θ(n^2)</code></td>
      <td><code class="red">O(n^2)</code></td>
      <td><code class="green">O(1)</code></td>
    </tr>
    <tr>
      <td><a href="http://en.wikipedia.org/wiki/Insertion_sort">Insertion Sort</a></td>
      <td><code class="yellow">Ω(n)</code></td>
      <td><code class="red">Θ(n^2)</code></td>
      <td><code class="red">O(n^2)</code></td>
      <td><code class="green">O(1)</code></td>
    </tr>
    <tr>
      <td><a href="http://en.wikipedia.org/wiki/Selection_sort">Selection Sort</a></td>
      <td><code class="red">Ω(n^2)</code></td>
      <td><code class="red">Θ(n^2)</code></td>
      <td><code class="red">O(n^2)</code></td>
      <td><code class="green">O(1)</code></td>
    </tr>
    <tr>
      <td><a href="https://en.wikipedia.org/wiki/Tree_sort">Tree Sort</a></td>
      <td><code class="orange">Ω(n log(n))</code></td>
      <td><code class="orange">Θ(n log(n))</code></td>
      <td><code class="red">O(n^2)</code></td>
      <td><code class="yellow">O(n)</code></td>
    </tr>
    <tr>
      <td><a href="http://en.wikipedia.org/wiki/Shellsort">Shell Sort</a></td>
      <td><code class="orange">Ω(n log(n))</code></td>
      <td><code class="red">Θ(n(log(n))^2)</code></td>
      <td><code class="red">O(n(log(n))^2)</code></td>
      <td><code class="green">O(1)</code></td>
    </tr>
    <tr>
      <td><a rel="tooltip" title="Only for integers. k is a number of buckets" href="http://en.wikipedia.org/wiki/Bucket_sort">Bucket Sort</a></td>
      <td><code class="green">Ω(n+k)</code></td>
      <td><code class="green">Θ(n+k)</code></td>
      <td><code class="red">O(n^2)</code></td>
      <td><code class="yellow">O(n)</code></td>
    </tr>
    <tr>
      <td><a rel="tooltip" title="Constant number of digits 'k'" href="http://en.wikipedia.org/wiki/Radix_sort">Radix Sort</a></td>
      <td><code class="green">Ω(nk)</code></td>
      <td><code class="green">Θ(nk)</code></td>
      <td><code class="green">O(nk)</code></td>
      <td><code class="yellow">O(n+k)</code></td>
    </tr>
    <tr>
      <td><a rel="tooltip" title="Difference between maximum and minimum number 'k'" href="https://en.wikipedia.org/wiki/Counting_sort">Counting Sort</a></td>
      <td><code class="green">Ω(n+k)</code></td>
      <td><code class="green">Θ(n+k)</code></td>
      <td><code class="green">O(n+k)</code></td>
      <td><code class="yellow">O(k)</code></td>
    </tr>
    <tr>
      <td><a href="https://en.wikipedia.org/wiki/Cubesort">Cubesort</a></td>
      <td><code class="yellow">Ω(n)</code></td>
      <td><code class="orange">Θ(n log(n))</code></td>
      <td><code class="orange">O(n log(n))</code></td>
      <td><code class="yellow">O(n)</code></td>
   </tr>

</table>